Confidential Transactions from Basic Principles
During my time at NCC Group this summer, I had the opportunity to dig into all sorts of cryptocurrency software to see how they work and what kind of math they rely on. One sought-after property that some cryptocurrencies (ZCash, Monero, all CryptoNote-based coins) support is confidential transactions. To explain what this means, we’ll first look at what Bitcoin transactions do.
At its core, a Bitcoin transaction is just a tuple (\(\{a_i\}, \{b_i\}, \{v_i\})\) where \(\{a_i\}\) are the input addresses, \(\{b_i\}\) are the output addresses, and \(\{v_i\}\) are the amounts that go to each output. We’ll ignore the proof-of-work aspect, since it isn’t quite relevant to where we’re going with this. Each transaction appears unencrypted for the whole world to see in the public ledger. This is all well and good, but it makes transactions easy to trace, even when the coins go through multiple owners. One way to make this harder is to use a tumbler, which essentially takes in Bitcoin from many sources, mixes them around, and hands back some fresh uncorrelated coins (you might be familiar with this concept under the term “money laundering”).
The goal of confidential transactions is to let just the participants of a transactions see the \(v_i\) values, and otherwise hide them from the rest of the world. But at the same time, we want non-participants to be able to tell when a transaction is bogus. In particular, we don’t want a user to be able to print money by spending more than they actually have. This property was easily achieved in the Bitcoin scheme, since the number of Bitcoin in each address \(a_i\) is publicly known. So a verifier need only check that the some of the outputs doesn’t exceed the sum of account contents of the input addresses. But how do we do this when the account contents and the output values are all secret? To show how, we’ll need a primer in some core cryptographic constructions. There is a lot of machinery necessary to make this work, so bear with me.
Schnorr Signatures
The purpose of a signature is to prove to someone who knows your public information that you have seen a particular value. In the case of Schnorr Signatures, I am working in an abelian group \(\mathbb{G}\) of prime order \(q\) with generator \(G\) (more generally, I guess this is a vector space that’s also a group) and I have a public key \(P = xG\) where \(x \in \mathbb{Z}_q\) is my secret key.
First, we’ll start off with Schnorr proof of knowledge. I would like to prove to a verifier that I know the value of \(x\) without actually revealing it. Here’s how I do it:
- First, I pick a random \(\alpha \leftarrow \mathbb{Z}_q\) and send \(Q = \alpha G\) to the verifier.
- The verifier picks \(e \leftarrow \mathbb{Z}_q\) and sends it to me.
- I calculate \(s = \alpha - ex\) and send \(s\) to the verifier.
-
Lastly, the verifier checks that \(sG + eP = Q\). Note that if all the other steps were performed correctly, then indeed
\[sG + eP = (\alpha - ex)G + exG = \alpha G - exG + exG = \alpha G = Q\]
We can quickly prove that this scheme is sound in the sense that being able to consistently pass verification implies knowledge of the secret \(x\). To prove this, it suffices to show that an adversary with access to such a prover \(P\) and the ability to rewind \(P\) can derive \(x\) efficiently. Suppose I have such a \(P\). Running it the first time, I give it any value \(e \leftarrow \mathbb{Z}_q\). \(P\) will return its proof \(s\). Now I rewind \(P\) to just before I sent \(e\). I send a different value \(e’ \neq e\) and receive its proof \(s’\). With these two values, I can easily compute
\[\frac{s - s'}{e' - e} = \frac{\alpha - ex - \alpha + e'x}{e' - e} = \frac{x(e' - e)}{e' - e} = x\]and, voilà, the private key is exposed.
Ok that was pretty irrelevant for where I’m going, but I thought it was a nice quick proof. So how can we use proof of knowledge to construct a signature? Well we can tweak the above protocol in order to “bind” our proofs of knowledge to a particular message \(M \in \{0,1\}^* \). The trick is to use \(M\) in the computation of \(e\). This also makes the interactivity of this protocol unnecessary. That is, since I am computing \(e\) myself, I don’t need a challenger to give it to me. But be careful! If we are able to pick \(e\) without any restrictions in our proof-of-knowledge algorithm, then we can “prove” we know the private key to any public key \(P\) by first picking random \(e\) and \(s\) and then retroactively letting \(Q = sG + eP\). So in order to prevent forgery, \(e\) must be difficult to compute before \(Q\) is determined, while also being linked somehow to \(M\). For this, we make use of a hash function \(H: \{0,1\}^* \to \mathbb{Z}_q\). Here’s how the algorithm to sign \(M \in \{0,1\}^* \) goes. Note that because this no longer interactive, there is no verifier giving me a challenge:
- I pick a random \(\alpha \leftarrow \mathbb{Z}_q\) and let \(Q = \alpha G\).
- I compute \(e = H(Q \,||\, M)\)
- I compute \(s = \alpha - ex\)
- I return the signature, which is the tuple \(\sigma = (s, e)\)
Observe that because hash functions are difficult to invert, this algorithm essentially guarantees that \(e\) is determined after \(Q\). To verify a signature \((s, e)\) of the message \(m\), do the following:
- Let \(Q = sG + eP\)
- Check that \(e = H(Q \,||\, M)\)
Fantastic! We’re now a fraction of the way to confidential transactions! The next step is to extend this type of proof to a context with multiple public keys.
(Extra credit: prove that Schnorr is sound in the Random Oracle Model. That is, assume an adversary has the ability to run and rewind the prover \(P\) as before, but now also has to ability to intercept queries to \(H\) and return its own responses, as long as those responses are random and consisent with responses on the same query input)
AOS Ring Signatures
The signatures that end up being used in confidential transactions are called ring signatures. It’s the same idea as a regular signature, except less specific: a ring signature of the message \(m\) over the public keys \(\{P_1, P_2, \ldots, P_n\}\) proves that someone with knowledge of one of the private keys \(\{x_1, x_2, \ldots, x_n\}\) has seen the message \(m\). So this is a strict generalization of the signatures above, since regular signatures are just ring signatures where \(n=1\). Furthermore, it is generally desired that a ring signature not reveal which private key it was that performed the signature. This property is called signer ambiguity.
The Abe, Okhubo, Suzuki ring signature scheme is a generalization of Schnorr Signatures. The core idea of scheme is, for each public key, we compute an \(e\) value that depends on the previous \(Q\) value, and all the \(s\) values are random except for the one that’s required to “close” the ring. That “closure” is performed on the \(e\) value whose corresponding public key and private key belong to us.
I’ll outline the algorithm in general and then give a concrete example. Denote the public keys by \(\{P_1, \ldots, P_n\}\) and let \(x_j\) be the private key of public key \(P_j\). An AOS signature of \(M \in \{0,1\}^* \) is computed as follows:
- Pick \(\alpha \leftarrow \mathbb{Z}_q\). \(Q = \alpha G\) and let \(e_{j+1} = H(Q \| M)\).
- Starting at \(j+1\) and wrapping around the modulus \(n\), for each \(i \neq j\), pick \(s_i \leftarrow \mathbb{Z}_q \) and let \(e_{i+1} = H(s_iG + e_iP_i \,\|\, M)\)
- Let \(s_j = \alpha - e_jx_j\)
- Output the signature \(\sigma = (e_0, s_0, s_1, \ldots, s_n)\).
That’s very opaque, so here’s an example where there are the public keys \(\{P_0, P_1, P_2\}\) and I know the value of \(x_1\) such that \(P_1 = x_1G\):
- I start making the ring at index 2: \(\alpha \leftarrow \mathbb{Z}_q \). \(e_2 = H(\alpha G \,||\, M)\).
- I continue making the ring. \(s_2 \leftarrow \mathbb{Z}_q \). \(e_0 = H(s_2 G + e_2 P_2 \,||\, M) \).
- I continue making the ring. \(s_0 \leftarrow \mathbb{Z}_q \). \(e_1 = H(s_0 G + e_0 P_0 \,||\, M) \).
- Now notice that \(e_2\) has been determined in two ways: from before, \(e_2 = H(\alpha G\,||\, M)\), and also from the property which must hold for every \(e\) value: \(e_2 = H(s_1 G + e_1 P_1\,||\, M)\). The only \(s_1\) that satisfies these constraints is \(s_1 = \alpha - e_1x_1\), which I can easily compute, since I know \(x_1\).
- Finally, my signature is \(\sigma = (e_0, s_0, s_1, s_2)\).
The way to verify this signature is to just step all the way through the ring until we loop back around, and then check that the final \(e\) value matches the initial one. Here are steps for the above example; the general process should be easy to see:
- Let \(e_1 = H(s_0 G + e_0 P_0 \,||\, M) \).
- Let \(e_2 = H(s_1 G + e_1 P_1 \,||\, M) \).
- Let \(e’_0 = H(s_2 G + e_2 P_2 \,||\, M) \).
- Check that \(e_0 = e’_0\).
The verification process checks that some \(s\) value was calculated after all the \(e\) values were determined, which implies that some secret key is known. Which \(s\) it is is well-hidden, though. Notice that all the \(s\) values but the last one are random. And also notice that the final \(s\) value has \(\alpha\) as an offset. But that \(\alpha\) was chosen randomly and was never revealed. So this final \(s\) value is completely indistinguishable from randomness, and is thus indistinguishable from the truly random \(s\) values. Pretty cool, huh?
There’s one tweak we can make to this that’ll slightly improve efficiency and make notation easier. Including \(M\) at every step really isn’t necessary. It just has to get mixed in at some point in the process. A natural place to put it is in \(e_0 = H(s_{n-1} G + e_{n-1} P_{n-1} \,\|\, M)\) and calculate the other \(e\) values without the \(m\), like \(e_{i+1} = H(s_iG + e_iP_i)\).
Borromean Ring Signatures
If you thought we were done generalizing, you’re dead wrong. We’ve got one more step to go. Consider the following situation (and withhold your cries for practical application for just a wee bit longer): there are multiple sets of public keys \(\mathcal{A}_1, \mathcal{A}_2, \mathcal{A}_3 \). I, having one private key in each \(\mathcal{A}_i \), would like to sign a message \(M\) in each of these rings. In doing so, I am proving “Some key in \(\mathcal{A}_1 \) signed \(M\) AND some key in \(\mathcal{A}_2 \) signed \(M\) AND some key in \(\mathcal{A}_3 \) signed \(M\).” The naïve approach is to make a separate AOS signature for each set of public keys, giving us a final signature of \(\sigma = (\sigma_1, \sigma_2, \sigma_3)\). But it turns out that there is an (admittedly small) optimization that can make the final signature smaller.
Gregory Maxwell’s Borromean ring signature scheme1 makes the optimization of pinning \(e_0\) as a shared \(e\) value for all rings \(\mathcal{A}_i\). More specifically, the paper defines
\[e_0 = H(R_0 \| R_1 \| \ldots \| R_{n-1} \| M)\]where each \(R_i = s_{i, m_i-1} G + e_{i, m_i-1} P_{i, m_i-1}\) when \(j_i \neq m_i-1\), and \(R_i = \alpha_i G\) otherwise, and \(m_i\) denotes the number of public keys in the \(i^\textrm{th}\) ring, and \(j_i\) denotes the index of the known private key in the \(i^\textrm{th}\) ring. The whole \(R\) thing is a technicality. The gist is that the last \(e\) and \(s\) values of every ring (whether it correspond to the known private key or not) are incorporated into \(e_0\). Here’s a pretty picture from the Maxwell Paper to aide your geometric intuition (if one believes in such silly things)
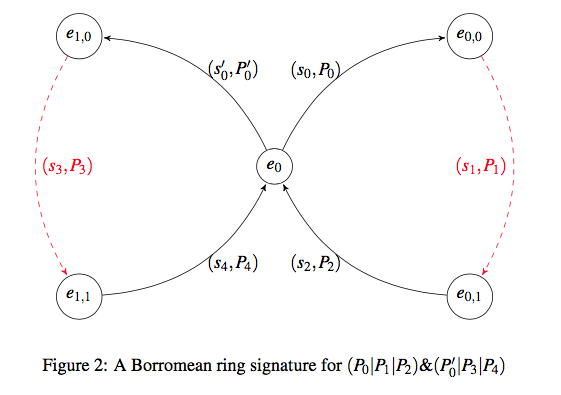
The signature itself looks like
\[\sigma = (e_0, (s_{0,0}, s_{0,1}, \ldots, s_{1,m_0-1}), \ldots, (s_{n-1,0}, \ldots, s_{n-1,m_{n-1}-1}))\]where \(s_{i,j}\) is the \(j^\textrm{th}\) \(s\) value in the \(i^\textrm{th}\) ring.
For clarity, I did slightly modify some details from this paper, but I don’t believe that the modifications impact the security of the construction whatsoever. There is also the important detail of mixing the ring number and position in the ring into at least one \(e\) value per-ring so that rings cannot be moved around without breaking the signature. The mixing is done by simply hashing the values into some \(e\).
Anyway, the end result of this construction is a method of constructing \(n\) separate ring signatures using \(\sum m_i + 1\) values (the \(s\) values plus the one \(e_0\)) instead of the naïve way, in which we would have to include \(e_{0,0}, e_{1,0}, \ldots, e_{n-1,0}\). This saves us \(n-1\) integers in the signature.
You might be wondering how large \(n\) is that such savings are worth a brand-new signature scheme. If you are wondering that, stop reading, because you won’t get an answer. Onwards towards more theory!
Pedersen Commitments
Alright, we have all the signature technology we need. Now let’s turn that fear of math into fear of commitment(s). A commitment is a value that is published prior to the revealing of some information. The commitment proves that you knew that information before it was revealed. Suppose I wanted to prove to someone that I know the winner of tomorrow’s horse race, but I don’t want to tell them because they might make a massive bet and raise suspicion. I could tweet out the SHA256 hash
1c5d6a56ec257e5fe6f733e7e81f6f2571475d44c09faa9ecdaa2ff1c4a49ecd
Once the race is over, I tweet again, revealing that the preimage of the hash was “Cloud Computing”. Since finding the preimage of a hash function is capital-D-Difficult, I have effectively proven that I knew ahead of time that Cloud Computing would win (note: the set of possible winners is so small that someone can easily just try all the names and see what matches. In this case, I would pick a random number and commit to “Cloud Computing.ba9fd6d66f9bd53d” and then reveal that later.)
Pedersen commitments are a type of commitment scheme with some nice properties that the hashing technique above doesn’t have. A Pedersen commitment in an abelian group \(\mathbb{G}\) of prime order \(q\) requires two public and unrelated generators, \(G\) and \(H\) (by unrelated, I mean there should be no obvious relation \(aG = H\)). If I want to commit to the value \(v \in \mathbb{Z}_q \) I do as follows:
- Pick a random “blinding factor” \(\alpha \leftarrow \mathbb{Z}_q \).
- Return \(Q = \alpha G + v H\) as my commitment.
That’s it. The way I reveal my commitment is simply by revealing my initial values \((\alpha, v)\). It’s worth it to quickly check that the scheme is binding, that is, if I make a commitment to \((\alpha, v)\), it’s hard to come up with different values \((\alpha’, v’)\) that result in the same commitment. For suppose I were able to do such a thing, then
\[\alpha G + v H = \alpha' G + v' H \implies (\alpha - \alpha')G = (v' - v)H \implies G = \frac{v' - v}{\alpha - \alpha'}H\]and we’ve found the discrete logarithm of \(H\) with respect to G, which we assumed earlier was hard. Another cool property (which is totally unrelated to anything) is perfect hiding. That is, for any commitment \(Q\) and any value \(v\), there is a blinding factor \(\alpha\) such that \(Q\) is a valid commitment to \((\alpha, v)\). This is just by virtue of the fact that, since \(G\) is a generator, there must be an \(\alpha\) such that \(\alpha G = Q - vH\) (also since \(H\) is also a generator, this also works if you fix \(Q\) and \(\alpha\) and derive \(v\)). Perfect hiding proves that, when \(\alpha\) is truly random, you cannot learn anything about \(v\), given just \(Q\).
Lastly, and very importantly, Pedersen commitments are additively homomorphic. That means that if \(Q\) commits to \((\alpha, v)\) and \(Q’\) commits to \((\alpha’, v’)\), then
\[Q + Q' = \alpha G + vH + \alpha' G + v'H = (\alpha + \alpha')G + (v + v')H\]So the commitment \(Q + Q’\) commits to \((\alpha + \alpha’, v + v’)\). We’ll use this property in just a second.
Hiding Transaction Amounts
Ok so back to the problem statement. We’ll simplify it a little bit. A transaction has an input amount \(a\), an output amount \(b\), and a transaction fee \(f\), all in \(\mathbb{Z}_q\). To maintain consistency, every transaction should satisfy the property \(a = b + f\), i.e., total input equals total output, so no money appears out of thin air and no money disappears into nothingness. We can actually already prove that this equation is satisfied without revealing any of the values by using Pedersen commitments. Pick random \(\alpha_a \leftarrow \mathbb{Z}_q,\, \alpha_b \leftarrow \mathbb{Z}_q\), and let \(\alpha_f = \alpha_a - \alpha_b\). Now make the Pedersen commitments
\[P = \alpha_a G + aH \quad Q = \alpha_b G + bH \quad R = \alpha_f G + fH\]and publish \((P,Q,R)\) as your transaction. Then a verifier won’t be able to determine any of the values of \(a\), \(b\), or \(f\), but will still be able to verify that
\[P - Q - R = (\alpha_a - \alpha_b - \alpha_f) G + (a - b - f)H = 0G + 0H = \mathcal{O}\]Remember, if someone tries to cheat and picks values so \(a - b - f \neq 0\), then they’ll have to find an \(\alpha\) such that \(-\alpha G = (a - b - f) H\) which is Hard. So we’re done, right? Problem solved! Well not quite yet. What we actually have here is a proof that \(a - b - f \equiv 0\, (\textrm{mod } q)\). See the distinction? For example, let \(q\) be a large prime, say, 13. I’ll have the input to my transaction be 1🔥TC (Litcoin; ICO is next week, check it out). I’d like to print some money, so I set my output to be 9🔥TC. I’ll be generous and give the miner 5🔥TC as my fee. Then anyone can check via the generated Pedersen commitments that
\[a - b - f = 1 - 9 - 5 = -13 \equiv 0\, (\textrm{mod } 13)\]So this transaction passes the correctness test. What happened? I overflowed and ended up wrapping around the modulus. Since all our arithmetic is done modulo \(q\), none of the above algorithms can tell the difference! So how can we prevent the above situation from happening? How do I prove that my inputs don’t wrap around the modulus and come back to zero? One word:
Rangeproofs
To prove that our arithmetic doesn’t wrap around the modulus, it suffices to prove that the values \(a,b,f\) are small enough such that their sum does not exceed \(q\). To avoid thinking about negative numbers, we’ll check that \(a = b + f\) instead of \(a - b - f = 0\), which are identical equations, but the first one will be a bit easier to reason about. To show that \(b + f < q\), we will actually show that \(b\) and \(f\) can be represented in binary with \(k\) bits, where \(2^{k+1} < q\) (this ensures that overflow can’t happen since \(b,f < 2^k\) and \(2^k + 2^k = 2^{k+1} < q\)). In particular, for both \(b\) and \(f\), we will make \(k\) Pedersen commitments, where each \(v\) value is provably 0 or a power of two, and the sum of the commitments equals the commitment of \(b\) or \(f\), respectively. Let’s do it step by step.
- I start with a value \(v\) that I want to prove is representable with \(k\) bits. First, pick a random \(\alpha \leftarrow \mathbb{Z}_q\) and make a Pedersen commitment \(P = \alpha G + v H\)
- Break \(v\) down into its binary representation: \(v = b_0 + 2b_1 + \ldots + 2^{k-1}b_{k-1} \).
-
For each summand, make a Pedersen commitment, making sure that the sum of the commitments is \(P\). That is,
\[\forall 0 \leq i < k-1 : \textrm{pick } \alpha_i \leftarrow \mathbb{Z}_q, \quad \textrm{let } \alpha_{k-1} = \alpha - \sum_{i=0}^{k-2} \alpha_i\]Then for all \(i\), commit
\[P_i = \alpha_i G + 2^ib_i H\]This ensures that \(P = P_0 + P_1 + \ldots + P_{k-1}\). The verifier will be checking this property later.
Great. So far we’ve provably broken down a single number into \(k\) constituents, while hiding all the bits. But how does a verifier know that all the \(b\) values are bits? What’s preventing me from picking \(b_0 = 3^{200}\), for example? This is where we will use ring signatures! For each commitment, we’ll make the set \(\mathcal{A}_i = \{P_i, P_i - 2^iH\}\) and treat that as a set of public keys for a ring signature. Note that, because we know the binary expansion of \(v\), we know the private key to exactly one of the public keys in \(\mathcal{A}_i\). This is because
\[b_i = 0 \implies P_i = \alpha_i G + 0H = \alpha_i G\] \[b_i = 1 \implies P_i - 2^iH = \alpha_i G + 2^iH - 2^iH = \alpha_i G\]So to prove that \(b_i = 0 \textrm{ or } 1\), we construct a ring signature over \(\mathcal{A}_i\). Since the ring signature is signer-ambiguous, a verifier can’t determine which key did the signing. This means we get to hide all the bits, while simultaneously proving that they are indeed bits! We get some space savings by using Borromean signatures here, since we’ll have \(k\) total signatures of size 2 each. The final rangeproof of the value \(v\) is thus
\[R_v = (P_0, \ldots, P_k, e_0, s_0, \overline{s_0}, s_1, \overline{s_1}, \ldots, s_k, \overline{s_k})\]where \(s_i\) and \(\overline{s_i}\) are the \(s\) values of the \(i^\textrm{th}\) ring signature. Obviously, the choice of binary representation as opposed to, say, base-16 representation is arbitrary, since you can make rings as big as you want, where each public key corresponds to a digit in that representation. But note that the space savings that Borromean ring signatures give us come from the number of rings, not their size. So it appears to be a good strategy to make the rings as small as possible and let the center \(e_0\) value take the place of as many \(e\) values as possible.
Putting It All Together
So to recap, we have picked transaction input \(a\), output \(b\), and fee \(f\), and hidden them with Pedersen commitments \(P_a\), \(P_b\), and \(P_f\). This gives verifiers the ability to check correctness of the transaction up to modulus-wrapping. Then we constructed the commitments’ corresponding rangeproofs \(R_a\), \(R_b\), and \(R_f\) so that a verifier gets the last piece of assurance that the transaction is correct and there is no overflow. So, in total, a confidential transaction is the tuple
\[(P_a, P_b, P_f, R_a, R_b, R_f)\]And that’s how confidential transactions work! If I want to send 🔥TC to someone, I can construct a confidential transaction that I make public, and then privately reveal the commitments for \(P_a\), \(P_b\) and \(P_f\) so that they can be sure that I actually sent what I claim. Because the commitments are binding, they can be certain that I can’t claim to someone else that I sent different \(a\), \(b\) or \(f\) values.
There’s plenty more detail in how transactions are constructed that I didn’t cover, but I hope I was able to explain the core of confidential transactions, and hopefully interest you in cryptography a little bit more. There’s a lot of cool stuff out there, and cryptocurrencies are a massive playing field for novel constructions.
-
Sorry, you’re gonna have to compile the \(\LaTeX\) yourself. Every PDF on the internet is either outdated or erroneous. ↩
