The Longest Blockchain is not the Strongest Blockchain
Bitcoin was first popularized in Bitcoin: A Peer-to-Peer Electronic Cash System (2008). The paper1 has spawned a wide variety of systems that use a similar permissionless model for achieving consensus.
Bitcoin’s consensus algorithm, hereby referred to as “Nakamoto Consensus”, powers many cryptocurrencies today. The basic concept is simple, the state is organized into a tree structure, or “block tree.” Each node in the tree is a valid block of transactions, and blocks necessarily point to the previous block’s cryptographic hash. Nodes reach consensus by selecting a path in this tree of valid blocks. This is the basic structure which defines many cryptocurrencies.
In Nakamoto Consensus, “Proof-of-Work” defines a mechanism which enforces an easily verifiable but difficult to compute delay. Originally defined by Adam Back’s Hashcash paper 2, PoW is effectively used by many cryptocurrencies to place a control on the rate of block generation, and to provide a mechanism for block proposers (miners) to be chosen. Proof-of-Work is hard to produce and easy to verify. An algorithm exists for adjusting the “work” parameter, ensuring that the time to create each block maintains relatively constant.
Consensus can be reached by selecting the “longest” chain of valid blocks. In the Bitcoin whitepaper1, and some other documentation, it is indicated that the honest chain grows the longest, assuming that 51% or less of the miners are malicious. Therefore, the longest chain can be considered to be the chain with the most invested Proof-of-Work:
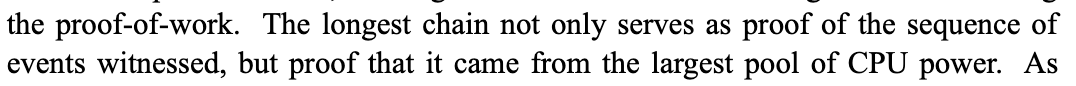
and later:

However, this conflation of “longest” with “greatest proof-of-work” is false, and reaching consensus by purely selecting the longest chain is not safe.
The difference is subtle, but in many common Blockchain designs, longer Proof-of-Work chains may exist that contain far less work. This is due to the fact that Proof-of-Work consensus is a probabilistic process controlled by mining difficulty. Mining difficulty is a function of timestamps, and hashrate is not constant. This ‘length vs weight’ misconception was present in Bitcoin’s initial implementation and was quickly fixed early on in the history of the popular cryptocurrency’s development.
Two General Attacks on Length and Weight confusion in Bitcoin
The Bitcoin whitepaper1 briefly outlines a framework for evaluating the probability of an attacker mining a longer chain than the “honest” chain, using a binomial random walk. However, this model fails to consider certain mechanics of the Proof-of-Work difficulty adjustment algorithm. We’ll show two attacks that both produce longer valid chains than the majority hashrate chain, without requiring 51% of the network hash rate.
Briefly: Difficulty Adjustment Algorithm
We’ll discuss the concept of a difficulty adjustment algorithm (DAA) in the general sense briefly here, since some understanding of how it functions is required to understand the two attacks outlined in this post. First, let’s take a look at how the work in Proof-of-Work is created:

Miners on a Proof-of-Work chain want to create a block that meets the difficulty
target. In other words, a block for which the first n bits of its hash are
zero. n acts as a difficulty parameter in this context. In Bitcoin this is
known as nBits, the block mining target threshold.
nBits exists because the difficulty of producing new blocks must scale with
the cumulative mining power of the participants in Proof-of-Work mining. We
want new blocks to be generated at a constant frequency, known as a ‘block
time’, regardless of how many participants and how much power is actively
mining at a given moment. Hence, the concept of a “difficulty adjustment
algorithm.”
Time is a tricky subject in distributed systems, in that it doesn’t really exist. There are block/sequence numbers, how many times a given consensus mechanism has been run, etc, but coming to an agreement across all participants about some absolute earth time is hard.
In order to maintain a constant ‘block-time’, the difficulty adjustment algorithm computes the time taken by the previous blocks within the adjustment period. Then, the difficulty parameter can be scaled by how much over, or under, the average block time was over the adjustment period. The source of ‘time’ in this context is from the timestamps added to each block by miners. Miners may choose any timestamp that meets the validation rules for timestamps.
Longer Chain via Timestamp Manipulation
The first of two example attacks outlined here to achieve a longer, less-heavy Proof-of-Work chain is as follows. It exploits the mechanics of timestamp validation rules in order to produce a long, weak chain on an isolated network, which can then be broadcast to “take over” the network state assuming the validation rules follow the “longest chain” rule.
The attack takes the following form in the general case:
-
Attacker forks the chain from a point where the difficulty is low, such as the genesis block. Keeps this fork isolated, never broadcasting its blocks.
-
Attacker mines blocks locally, and manipulates the block timestamps so that the block time appears to be far too long.
-
Each difficulty adjustment period will cause a decrease in difficulty, since the timestamps have been manipulated to trick the DAA into lowering the difficulty.
-
The chain will quickly become longer than the main, ‘legitimate’ chain, despite containing far less work.
-
Attacker broadcasts the long, weak chain and takes over the network state, performing a double spend attack or simply allocating themselves all of the block rewards.
The feasibility of this approach depends on how new block timestamps are validated, in addition to requiring the ‘length vs weight’ equivalence assumption. In the case of Bitcoin, new blocks are validated by checking that they are greater than the median of the previous 11 blocks, but less than the average system time returned to you by your peers. In the case of isolated mining, you can configure all of your peers to return an extremely high timestmap, bypassing this check. Variations of this attack have been exploited and led to real world losses 3. Nodes should always perform robust timestamp validation in addition to assessing the longest fork correctly.
Longer Chain via Hashrate Increase
The second attack we can execute which violates the assumed equivalence between longest and strongest chain is as follows. Note that this attack does not require 51% of the hash rate and is different from the standard 51% attack.
Most difficulty adjustment algorithms have a discrete adjustment period, the number of blocks in between adjustments. Bitcoin’s difficulty adjustment algorithm readjusts the mining difficulty parameter once every 2016 blocks. This means that, if the network hashrate abruptly increases or decreases inside this window, the block time will be unadjusted and blocks will be produced faster, or slower, than expected.
So, the second attack to create a longer, but lighter, chain is:
-
Fork from a point on the chain where there is low difficulty, such as the genesis block.
-
Mine on the isolated chain, significantly increasing the hash rate after each difficulty adjustment (by 4x, for example), causing the average block time to be consistently lower than the target on average.
-
Eventually, the attacker chain will catch up to the main chain, assuming the main chain is not too far ahead.
-
Broadcast the attacker chain.
This attack has limitations; it requires a significant amount of mining work to be invested (but still less than the assumed 51% required) and that the chain is not very old. Regardless of the practical exploitability of this technique, it is one way a valid longer chain can be produced, which has less mining difficulty. The Bitcoin testnet is another example of this property: it has a much higher block count despite having far less mining work, due to the high hashrate variance.
The Fix
The correct method for selecting the current state from the tree of valid blocks
linked together by Proof-of-Work is to compute the cumulative amount of work
required to produce the chain, and select the chain with the highest cumulative
work. In the case of Bitcoin and other Proof-of-Work cryptocurrencies that use an nBits
target threshold, this can be computed by taking:
sum(chain):
work := 0
for each block in chain:
work += 1<<bitSize / (block.nBits+1)
return work
This fix was implemented early on in Bitcoin’s history here: https://github.com/bitcoin/bitcoin/commit/40cd0369419323f8d7385950e20342e998c994e1#diff-23cfe05393c8433e384d2c385f06ab93R1129.
Conclusion
This length and weight confusion remains a common misconception about Nakamoto Consensus. Consensus protocols are complex, and many edge cases that may seem innocuous can have drastic consequences. Blockchain developers should carefully consider possible attacks against their consensus scheme, adopting a defensive mindset and learning from previous mistakes encountered in common consensus systems. I’ve created simulations of the attacks described in the post, which are available on GitHub.
