Code Execution In Spite Of BitLocker
Disk Encryption is “a litany of difficult tradeoffs and messy compromises” as our good friend and mentor Tom Ptacek put it in his blog post. That sounds depressing, but it’s pretty accurate - trying to encrypt an entire hard drive is riddled with constraints. For example:
- Disk Encryption must be really, really fast. Essentially, if the crypto happens slower than the disk read speed (said another way, if the CPU is a bottleneck) - your solution is untenable to the mass market
- It must support random read and write access - any sector may be read at any time, and any sector may be updated at any time
- You really need to avoid updating multiple sectors for a single write - if power is lost during the operation, the inconsistencies will not be able to be resolved easily, if at all
- People expect hard disks to provide roughly the amount of advertised space. Stealing significant amounts of space for ‘overhead’ is not feasible. (This goes doubly so if encryption is applied after operating system installation - there may not be space to steal!)
The last two constraints mean that the ciphertext must be the exact same size as the plaintext. There’s simply no room to store IVs, nonces, counters, or authentication tags. And without any of those things, there’s no way to provide cryptographic authentication in any of the common ways we know how to provide it. No HMACs over the sector and no room for a GCM tag (or OCB, CCM, or EAX, all of which expand the message). Which brings us to…
Poor-Man’s Authentication
Because of the constraints imposed by the disk format, it’s extremely difficult to find a way to correctly authenticate the ciphertext. Instead, disk encryption relies on ‘poor-man’s authentication’.
The best solution is to use poor-man’s authentication: encrypt the data and trust to the fact that changes in the ciphertext do not translate to semantically sensible changes to the plaintext. For example, an attacker can change the ciphertext of an executable, but if the new plaintext is effectively random we can hope that there is a far higher chance that the changes will crash the machine or application rather than doing something the attacker wants.
We are not alone in reaching the conclusion that poor-man’s authentication is the only practical solution to the authentication problem. All other disk-level encryption schemes that we are aware of either provide no authentication at all, or use poor-man’s authentication. To get the best possible poor-man’s authentication we want the BitLocker encryption algorithm to behave like a block cipher with a block size of 512–8192 bytes. This way, if the attacker changes any part of the ciphertext, all of the plaintext for that sector is modified in a random way.
That excerpt comes from an excellent paper by Niels Ferguson of Microsoft in 2006 explaining how BitLocker works. The property of changing a single bit, and it propagating to many more bits, is diffusion and it’s actually a design goal of block ciphers in general. When talking about disk encryption in this post, we’re going to use diffusion to refer to how much changing a single bit (or byte) on an encrypted disk affects the resulting plaintext.
BitLocker in Windows Vista & 7
When BitLocker was first introduced, it operated in AES-CBC with something called the Elephant Diffuser. The BitLocker paper is an excellent reference both on how Elephant works, and why they created it. At its heart, the goal of Elephant is to provide as much diffusion as possible, while still being highly performant.
The paper also includes Microsoft’s Opinion of AES-CBC Mode used by itself. I’m going to just quote:
Any time you want to encrypt data, AES-CBC is a leading candidate. In this case it is not suitable, due to the lack of diffusion in the CBC decryption operation. If the attacker introduces a change d in ciphertext block i, then plaintext block i is randomized, but plaintext block i + 1 is changed by d. In other words, the attacker can flip arbitrary bits in one block at the cost of randomizing the previous block. This can be used to attack executables. You can change the instructions at the start of a function at the cost of damaging whatever data is stored just before the function. With thousands of functions in the code, it should be relatively easy to mount an attack.
The current version of BitLocker [Ed: BitLocker in Vista and Windows 7] implements an option that allows customers to use AES-CBC for the disk encryption. This option is aimed at those few customers that have formal requirements to only use government-approved encryption algorithms. Given the weakness of the poor-man’s authentication in this solution, we do not recommend using it.
BitLocker in Windows 8 & 8.1
BitLocker in Windows 8 and 8.1 uses AES-CBC mode, without the diffuser, by default. It’s actually not even a choice, the option is entirely gone from the Group Policy Editor. (There is a second setting that applies to only “Windows Server 2008, Windows 7, and Windows Vista” that lets you choose Diffuser.) Even using the commandline there’s no way to encrypt a new disk using Diffuser - Manage-BDE says “The encryption methods aes128_Diffuser and aes256_Diffuser are deprecated. Valid volume encryption methods: aes128 and aes256.” However, we can confirm that the code to use Diffuser is still present - disks encrypted under Windows 7 with Diffuser continue to work fine on Windows 8.1.
AES-CBC is the exact mode that Microsoft considered (quoting from above) “unsuitable” in 2006 and “recommended against”. They explicitly said “it should be relatively easy to mount an attack”.
And it is.
As written in the Microsoft paper, the problem comes from the fact that an attacker can modify the ciphertext and perform very fine-grained modification of the resulting plaintext. Flipping a single bit in the ciphertext results reliably scrambles the next plaintext block in an unpredictable way (the rainbow block), and flips the exact same bit in the subsequent plaintext block (the red line):
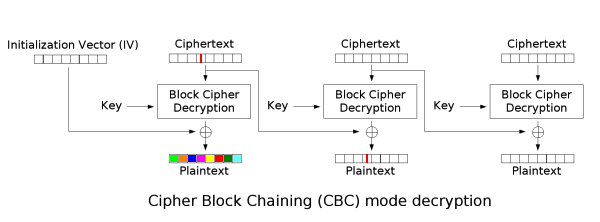
This type of fine-grained control is exactly what Poor Man’s Authentication is designed to combat. We want any change in the ciphertext to result in entirely unpredictable changes in the plaintext and we want it to affect an extremely large swath of data. This level of fine-grained control allows us to perform targeted scrambling, but more usefully, targeted bitflips.
But what bits do we flip? If the disk is encrypted, don’t we lack any idea of where anything interesting is stored? Yes and no. In our testing, two installations of Windows 8 onto the same format of machine put the system DLLs in identical locations. This behavior is far from guarenteed, but if we do know where a file is expected to be, perhaps through educated guesswork and installing the OS on the same physical hardware, then we will know the location, the ciphertext, and the plaintext. And at that point, we can do more than just flip bits, we can completely rewrite what will be decrypted upon startup. This lets us do much more than what people have suggested around changing a branch condition: we just write arbitrary assembly code. So we did. Below is a short video that shows booting up a Virtual Machine showing a normal unmodified BitLockered disk on Windows 8, shutting it down and modifying the ciphertext on the underlying disk, starting it back up, and achieving arbitrary code execution.
This is possible because we knew the location of a specific file on the disk (and therefore the plaintext), calculated what ciphertext would be necessary to write out desired shellcode, and wrote it onto the disk. (The particular file we chose did move around during installation, so we did ‘cheat’ a little - with more time investment, we could change our target to a system dll that hasn’t been patched in Windows Updates or moved since installation.) Upon decryption, 16 bytes were garbled, but we chose the position and assembly code carefully such that the garbled blocks were always skipped over. To give credit where others have demonstrated similar work, this is actually the same type of attack that Jakob Lell demonstrated against LUKS partitions last year.
XTS Mode
The obvious question comes up when discussing disk encryption modes: why not use XTS, a mode specifically designed for disk encryption and standardized and blessed by NIST? XTS is used in LUKS and Truecrypt, and prevents targeted bitflipping attacks. But it’s not perfect. Let’s look at what happens when we flip a single bit in ciphertext encrypted using XTS:
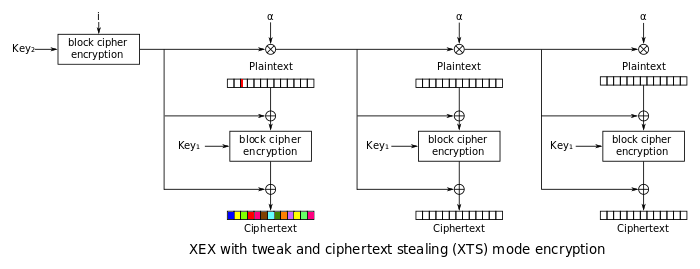
A single bit change completely scrambles the full 16 byte block of the ciphertext, there’s no control over the change. That’s good, right? It’s not bad, but it’s not as good as it could be. Unfortunately, XTS was not considered in the original Elephant paper (it was relatively new in 2006), so we don’t have their thoughts about it in direct comparison to Elephant. But the authors of Elephant evaluated another disk encryption mode that had the same property:
LRW provides some level of poor-man’s authentication, but the relatively small block size of AES (16 bytes) still leaves a lot of freedom for an attacker. For example, there could be a configuration file (or registry entry) with a value that, when set to 0, creates a security hole in the OS. On disk the setting looks something like “enableSomeSecuritySetting=1”. If the start of the value falls on a 16-byte boundary and the attacker randomizes the plaintext value, there is a 2−16 chance that the first two bytes of the plaintext will be 0x30 0x00 which is a string that encodes the ASCII value ’0’.
For BitLocker we want a block cipher whose block size is much larger.
Furthermore, they elaborate upon this in their comments to NIST on XTS, explicitly calling out the small amount of diffusion. A 16-byte scramble is pretty small. It’s only 3-4 assembly instructions. To compare how XTS’ diffusion compares to Elephant’s, we modified a single bit on the disk of a BitLockered Windows 7 installation that corresponded to a file of all zeros. The resulting output shows that 512 bytes (the smallest sector size in use) were modified:
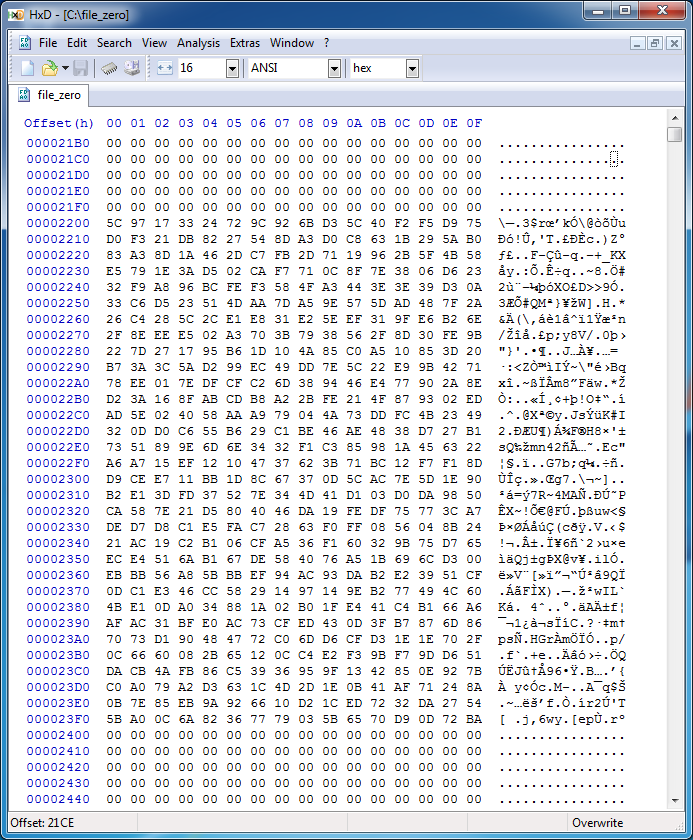
This amount of diffusion is obviously much larger than 16 bytes. It’s also not perfect - a 512 byte scramble, in the right location, could very well result in a security bypass. Remember, this is all ‘Poor Man’s Authentication’ - we know the solution is not particularly strong, we’re just trying to get the best we can. But it’s still a lot harder to pop calc with.
Conclusion
From talking with Microsoft about this issue, one of the driving factors in this change was performance. Indeed, when BitLocker first came out and was documented, the paper spends a considerable amount of focus on evaluating algorithms based on cycles/byte. Back then, there were no AES instructions built into processors - today there are, and it has likely shifted the bulk of the workload for BitLocker onto the Diffuser. And while we think of computers as becoming more powerful since 2006 - tablets, phones, and embedded devices are not the ‘exception’ but a major target market.
Using Full Disk Encryption (including BitLocker in Windows 8) is clearly better than not - as anyone’s who had a laptop stolen from a rental car knows. Ultimately, I’m extremely curious what requirements the new BitLocker design had placed on it. Disk Encryption is hard, and even XTS (standardized by NIST) has significant drawbacks. With more information about real-world design constraints, the cryptographic community can focus on developing something better than Elephant or XTS.
I’d like to thank Kurtis Miller for his help with Windows shellcode, Justin Troutman for finding relevant information, Jakob Lell for beating me to it by a year, DaveG for being DaveG, and the MSRC.
